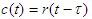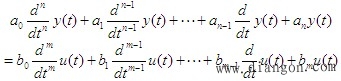1、控制系统的地位和要求
控制系统是机电一体化产品最重要的组成部分,相当于人的“大脑”,实现控制及信息处理功能。
对控制系统的基本要求:
被控制量按规定的规律变化,控制系统具备稳定性、快速性、准确性
2、控制系统的基本构成
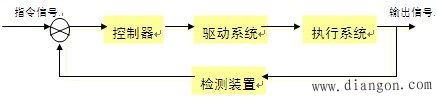
控制系统是由控制装置、执行机构、被控对象、检测装置所构成的整体,其基本构成如图所示:
被控对象可以是机电设备(如机床)、一种过程(如化工生产过程)等,它在控制装置的控制下,执行机构的驱动下,按预定的规律或目的运行。
简单的全自动洗衣机控制系统与复杂的航天飞机控制系统在原理上类似,但在结构上是很不相同的。如下图为线性处理及控制子系统的组成。
 3、控制系统的基本类型
3、控制系统的基本类型
根据机电一体化系统的多样性及复杂性决定了控制器的多样性,一般有以下四种类基本类型:
数字控制系统(NCS)
将被加工零件的几何信息和工艺信息数字化,按规定的代码和格式编成加工程序,由计算机生成数字形式的指令,再驱动机器运动的一种控制形式,其实际上是轨迹控制的问题。

控制介质:传递零件的加工信息
数控装置:完成信息的输入、存储、变换、运算及各种控制功能
伺服系统:接收指令驱动机床执行机构(即电信号到机械量转换)
检测装置:检测速度和位移,并反馈信息
伺服控制系统(SCS)
输入为模拟或数字的电信号,输出是机械的位移或速度的变化率,主要考虑如何稳定的、快速的、准确实现指令的功能要求,即要使输出量以一定的精度复现输入量的变化,常称为动作控制。
顺序控制系统
该系统采用开关控制方式,即输出量的开和关是一系列输入开关条件的函数。控制器对操作过程的“逻辑状态”进行控制,实现顺序控制的方法有机电式继电器、各种气动和

装置、可编程控制器(plc)等。
过程控制系统
在冶金、化工、电力等生产过程中采用的工业控制系统,过程控制系统的受控变量是生产过程的物理量,可以是连续的、离散的。
4、系统数学模型
控制系统的数学模型在控制系统的研究中有着相当重要的地位,要对系统进行仿真处理,首先应当知道系统的数学模型,然后才可以对系统进行模拟。
数学模型是描述元素之间、子系统之间、层次之间相互作用以及系统与环境相互作用的数学表达式。它是根据系统的动态特性,即通过决定系统特征的物理学定律,如机械�电气�热力�液压�

方面的基本定律而写成的。
(1)、输入――输出模型
对于输入――输出的数学模型,常用微分方程来描述该系统在时域中的动态特性。
(2)、状态模型
5、传递函数
建立系统数学模型的目的是为了对系统的性能进行分析。在给定外作用及初始条件下,求解微分方程就可以得到系统的输出响应。这种方法比较直观,特别是借助于电子计算机可以迅速而准确地求得结果。
设线性定常系统由下述阶线性常微分方程描述:
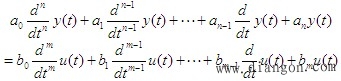
传递函数具有以下性质:
①传递函数是复变量的有理真分式函数,具有复变函数的所有性质。
②传递函数是系统或元件数学模型的另一种形式,是一种用系统参数表示输出量与输入量之间关系的表达式。
③传递函数与微分方程有相通性。
④传递函数的拉氏反变换是脉冲响应。
典型环节的传递函数:
一个物理系统是有许多元件组合而成的。虽然各种元件的具体结构和作用原理是多种多样的,但若抛开其具体结构和物理特点,研究其运动规律和数学模型的共性,就可以划分成为数不多的几种典型环节。
这些典型环节是:比例环节、微分环节、积分环节、比例微分环节、一阶惯性环节、二阶振荡环节和延迟环节。
(1)、比例环节
比例环节又称放大环节,其输出量与输入量之间的关系为一种固定的比例关系。这就是说,它的输出量能够无失真、无滞后地按一定的比例复现输入量
(2)、微分环节
微分环节是自动控制系统中经常应用的环节。微分环节的特点是在暂态过程中,输出量为输入量的微分
(3)、积分环节
积分环节的动态方程为
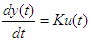
(4)、一阶惯性环节
自动控制系统中经常包含有这种环节,这种环节具有一个储能元件。
(5)、二阶振荡环节
二阶振荡环节的微分方程为

(6)、延迟环节
延迟环节的特点是,其输出信号比输入信号迟后一定的时间。其数学表达式为