二阶电路的方波响应实验原理

1.RLC电路的暂态响应

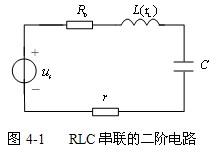
凡是可以用二阶微分方程描述的电路均称为二阶电路。二阶电路的响应也分为零输入响应、零状态响应和全响应。通过给二阶电路加入正方波电压源以观察电路的各种响应波形。RLC串联构成的二阶电路如图4-1所示。设各电压与取关联的顺时针方向，电路的总电阻，其中：为外接电阻，为电感线圈的电阻，为采样电阻。下面的响应以电容电压为例。

据KVL有，而， ，将其代人KVL得

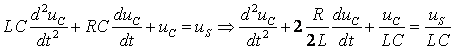
定义衰减系数（阻尼系数）：，谐振角频率： ，方程写为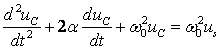

特征方程为

特征根为

定义为衰减振荡角频率为

根据特征根形式的不同，响应分为过阻尼、临界阻尼、欠阻尼、无阻尼四种情况：

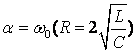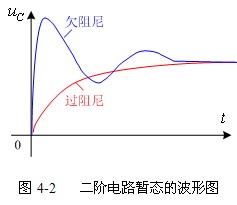
（1）当时，，为相等的负实根，响应为临界振荡。波形与过阻尼类似，是非振荡的，如图4-2所示。

（2）当时，，为不相等的实根。响应称为过阻尼。波形如图4-2所示。

（3）当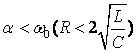时，，为一对共轭复数。响应称为欠阻尼。波形见图4-2所示。

（4）当时，为一对共轭复数。响应称为无阻尼。波形是一个角频率为的等幅振荡过程。

由上可见，RLC串联电路的响应类型仅与微分方程的系数有关，而与激励源无关。即响应类型仅与电路的元件参数有关。调节电路的参数就可以观察到各种响应类型。

2.对衰减系数(阻尼系数) 和衰减振荡角频率的测量

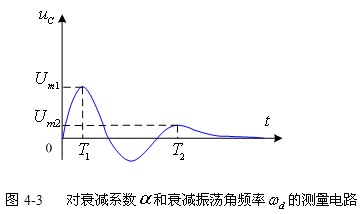
在欠阻尼的情况下，从欠阻尼振荡的波形可以计算衰减系数和衰减振荡角频率这两个参数。如图4-3所示波形为零输入情况下的欠阻尼的。其表示式为：。当时，；当时，，因此，

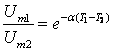
解得衰减系数，衰减振荡角频率。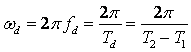

即通过用测量光标测量波形的和，便可求出和。

3.状态轨迹观察

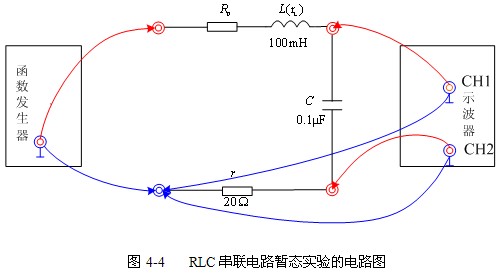
在图4-4所示电路的暂态过程中，若将电路的电压、电流在每一时刻的取值对应平面坐标系的一个点，这样得到的曲线称为电路的状态轨迹。电路的状态轨迹能反映电路的稳定状况。以图4-4所示电路的和为状态变量，用示波器观察电路状态轨迹的过程如下：将电路的输入示波器的CH1通道，输入示波器的CH2通道，示波器的显示方式设置为XY，则屏幕上显示的曲线就是该电路的状态轨迹。

调节电路的参数，分别观察电路在过阻尼和欠阻尼情况下的状态轨迹。

上述用示波器的CH2通道观察电流是通过采样电阻实现的。由于采样电阻的电压与流过它的电流同相位，数值上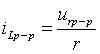，所以通过观察测量采样电阻的电压就可以得到电路的电流的相位和大小。为了使电路加入的采样电阻对原电路的影响可以忽略不计，一般要求，取值要远远小于与之串联的电路阻抗，且采样电阻的一端应接到信息源的地线端，以便整个电路实现“共地”，如图4-4所示。

相关内容推荐：

• 2017-01-06二阶电路的方波响应实验原理