1、耗量特性
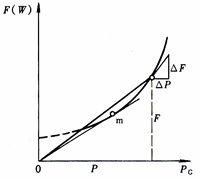
一台13．5万千瓦的小机组，比30万千瓦的机组耗煤要高15％左右，比60万千瓦的机组耗煤要高26％左右。 耗量特性――发电机组单位时间内能量输入和输出的关系。   耗量特性曲线上某点的纵、横坐标之比，即单位时间发电机组能量输入与输出之比，称为比耗量： μ=F/P G ，T/MW・hour (或g/kW・h) 或λ=W/P G ，m 3/MW・s 耗量特性曲线上某点切线的斜率，即单位时间发电机组能量输入增量与输出增量之比，称为该点的耗量微增率： λ=dF/dP G ，T/MW・h 或λ=dW/dP G ，m 3/MW・s 如果燃料耗量F(吨/小时)换成燃料费用成本F(元/小时)，则有“成本微增率”： λ=dF/dP G ，元/MW・h  2、同类型机组（发电厂）间的 有功负荷经济分配
有功负荷经济分配的目标：负荷一定时，各机组应如何分配有功负荷才能使单位时间的能源消耗量最小，即总耗量F Σ最小。  总耗量: F Σ = F 1 + F 2 功率平衡：P G1 + P G2 = P LΣ
或：P G1 + P G2 - P LΣ =0 F Σmin ←F Σ = F 1 + F 2
约束条件：P G1 + P G2 - P LΣ =0 条件极值问题可以用拉格郎日乘数法求解。 先建立拉格郎日函数： C *= F Σ -λ(P G1 + P G2 - P LΣ) λ――拉格郎日乘数。 拉格郎日函数极值点便是F Σ最小值条件。  注意：经济分配负荷时，除了等式约束外，还有不等式约束的限制：P Gimin≤P Gi ≤P Gimax。这时，可以先按“等耗量微增率准则”确定每台机组应发功率P Gi，如果某台k应发功率P Gk低于P Gkmin或高于P Gkmax，则取P Gk=P Gkmin或P Gk= P Gkmax，其它机组重新按“等耗量微增率准则”计算应发功率（总负荷变为： P LΣ - P Gk）。 ・该准则也适用于水电厂的有功负荷经济分配：  ・如果燃料耗量Fi(吨/小时)换成燃料费用成本F i(元/小时)，则有“等电能成本微增率准则”。  (￥/MW・h) ・也可考虑网损。 [例1]三个火电厂共同承担负荷，各电厂的燃料成本特性分别为： C 1=45+4P G1+0.01P 2G1 ￥/h 60MW≤ P G1 ≤90MW C 2=30+2P G2+0.03P 2G2 ￥/h 45MW≤ P G2 ≤100MW C 3=32+3P G3+0.008P 2G3 ￥/h 100MW≤ P G3 ≤155MW 当总负荷为300MW时，试确定每一个电厂承担的经济负荷值。 解：成本微增率为  按“等电能成本微增率准则”，有 4+0.02P G1=2+0.06P G2 ① 4+0.02P G1=3+0.016P G3 ② 功率平衡：P G1+P G2+PG3=300 ③ 4+0.02P G1=2+0.06P G2 ① 4+0.02P G1=3+0.016P G3 ② P G1+P G2+P G3=300 ③ 联立求解上列三式，求每一个电厂承担的经济负荷值： P G1=79.03MW 60MW≤ P G1 ≤90MW P G2=59.68MW 45MW≤ P G2 ≤100MW P G3=161.29MW 100MW≤ P G3 ≤155MW 所以只能取 P G3=155MW。 4+0.02P G1=2+0.06P G2 ① 取 P G3=155MW，则 P G1+P G2=300-155 ④ 联立求解式①、④，得： P G1=83.75MW P G2=61.25MW 60MW≤ P G1 ≤90MW 45MW≤ P G2 ≤100MW 100MW≤ P G3 ≤155MW | 