电源规划的数学模型

　　如前所述，电源规划的数学模型分为按发电机组优化的模型与按发电厂优化的模型两类。
　　目前，国际上一些通用的电源规划软件包大都采用按发电机组优化的数学模型，其中它们都选用了一个共同的简化假定，即电力系统的全部电力负荷与所有发电机组都被认为集中在一个节点上，因此又叫做单节点的数学模型。
　　这样就可以把同类发电机组合并在一起进行优化，使模型和算法大为简化。
　　显然，这种电源规划软件设计只能回答在什么时间扩建什么类型机组的问题，而不能回答在什么地方扩建这些机组的问题。
　　我国地域辽阔，一次能源分布和工业分布不均匀，其燃料基地主要在北方，丰富的水力资源则主要集中在西部，而大部分电力负荷却又在东南沿海地带。
　　在这种情况下，采用单节点的电源规划模型可能会引起较大误差。
　　此外，我国水力资源非常丰富，在当今能源紧张的情况下，合理利用水力发电在我国电力建设事业中占重要地位。为了充分反映水电的特点，在电源规划中应对水电站逐个进行优化排序，并在生产模拟中应分别进行处理。
　　因此，电源规划模型不仅应回答什么时间扩建什么类型机组的问题，还应该回答在何处扩建这些机组的问题。换言之，如果规划系统规模较大时，电源规划应按发电厂优化，而不应简单地按机组类型优化。
　　以下简单介绍一下单节点电源规划的数学模型。

　　当待扩建电力系统的负荷及一次能源分布比较均匀、厂址条件不受限制和原有输电网络较强时，使用这种电源规划模型能得到满意的结果。因为在这种情况下同一类型的发电机组有大致相同的技术经济指标，而输电网络的扩建费用对电源的结构与布局不致产生很大的影响。
　　按发电机组类型优化的电源规划在数学处理上比较简单。由于这类模型把同类型机组的发电厂都归并在一起，因而决策变量的个数大大减少。以下我们将以WASP为例介绍这类电源规划的数学模型。
　　WASP软件包能在满足给定的约束条件的情况下，寻求长达30年的发电系统最优扩建方案。该模型采用最小费用法作为经济评价的根据。
　　(一)目标函数
　　在单节点模型中，各方案的费用除了投资，燃料费及运行维修费以外，还包括停电损失费用。此外，考虑到各类机组使用寿命不同，投建时间不同，在规划期末将出现不同的剩余使用年限，所以应把有关投资项目的折余值当成残值处理，从总费用中减去。
　　目标函数为
　　
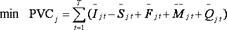
　　式中 　PVC_j ―规划方案总费用的现值；
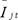
　　　　　　―投资费用；
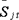
　　　　　　―投资的折余值；
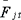
　　　　　　―燃料费用；
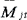
　　　　　　―运行维护费用；
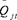
　　　　　　―停电损失费用；
　　下标jt―表示与方案j有关的费用在第t年的取值；
　　顶标“”―表示已将第t年有关费用按给定贴现率换算为某一时刻的现值；
　　T―规划期的总年数，又叫水平年。
　　显然，最优方案应为总费用现值最小的方案。
　　以下介绍目标函数中各项费用的具体计算方法。为了换算这些费用的现值，采取了以下的假定：
　　1）所有投资都在各年年初发生；
　　2）所有投资折余值都发生在水平年末；
　　3）燃料费用运行维护费用及停电损失费用都发生在各年度的中点。
　　因此，与电源规划有关的费用流可表现为图7-5的形式。根据图7-5即可计算 PVC_j 中各项费用。图7-5中的C,O分别表示投资和运行费用。
　　　　　
　　1．投资费用与折余费用
　　投资费用一般按概略指标估算,将其折算到基准年;
　　关于折余费用含义,设某机组使用寿命为n年,投资额为K,若规划水平年为T,而该机组在第t年投入使用,当T-t不等于n时,则存在剩余使用年,将此剩余年中的投资费用折算到水平年,即称为折余费用。
　　2．燃料费用
　　燃料费用计算也应考虑水文条件的影响,因为在不同水文条件下,其水电厂发电量不同,从而影响到火电厂机组出力情况。
　　总燃料费用由随机生产模拟求得,将费用设在年度中点发生较为合理。在计算中考虑了火电机组随机停运的影响，但对水电站则采用了强迫停运率为零的假定。
　　3．停运维修费用
　　包括固定运行维修费用和变动运行维修费用。
　　4．停电损失费用
　　停电损失包括直接停电损失和间接停电损失,计算停电损失费用需要考虑停电次数,停电持续时间以及系统本身由于停电增加的维检费用支出等。该项也是由随机生产模拟计算出电量不足期望值求得。
　　综上所述,以上每一项的费用计算都很麻烦,其中各项的费用计算公式详见参考使用教材。
　　(二)约束条件
　　单节点电源规划模型的约束条件包括电力平衡和可靠性约束条件。
　　其数学约束关系式的设置,以及相关的说明略。
　　以上只是对单节点电源规划模型作了简单介绍，实际上目标函数中的各项费用计算起来都很复杂和麻烦，并且要处理非常多的数据，必须借助计算机才能完成。虽然电源优化模型在求解算法及实际应用上，还有待于进一步的研究和探讨，但我们了解一下他的结构，特点及问题还是非常必要的。