一阶和二阶系统的数学模型

　　如果知道测量系统的数学模型，经过适当的运算，通常都可以推算得到该测量系统对任何输入的动态输出响应。但是测量系统的数学模型中的具体参数确定通常需经实验测定，亦称动态标定。工程上常用阶跃和正弦两种形式的信号作为标定信号。阶跃输入信号的函数表达式为

　　式中，A为阶跃输入信号幅值。

　　采用阶跃输入信号具有适用性广、实施简单、易于操作等特点。采用正弦输入信号对分析测量系统频率特性十分方便，但在对压力、流量、温度、物位等检测系统的实际应用中一般难以碰到被测参量以正弦方式变化的情况，可把被测参量随时间变化看作是在不同时刻一系列阶跃输入的叠加。工程上常见的各类检测系统的动态响应特性大都与理想的一阶或二阶系统相近，少数复杂系统也可近似地看作两个或多个二阶系统的串并联。

1．一阶系统的标准微分方程

　　不论是电学、力学，还是热工测量系统，其一阶系统的运动微分方程最终都可化成如下通式

　　　　　　　　　　　（1）

　　式中，Y（t）为测量系统的输出函数；x（t）为测量系统的输入函数；为测量系统的时间常数；k为测量系统的放大倍数。

　　上述一阶系统的传递函数表达式为

　　　　　　　　　　　（2）

　　上述一阶系统的频率特性表达式为

　　　　　　　　（3）

　　其幅频特性表达式为

　　　　　　　（4）

　　其相频特性表达式为

　　　　　　　　　　　　（5）

　2．二阶系统的标准微分方程

　　不论是电学、力学或热工测量系统，其二阶系统的运动微分方程最终都可化成如下通式

　　　　（6）

　　式中，为二阶系统的固有角频率；为二阶系统的阻尼比；K为二阶系统的放大倍数或称系统静态灵敏度。

　　上述二阶系统的传递函数表达式为

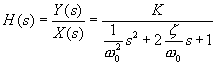　　　　　（7）

　　上述二阶系统的频率特性表达式为

　　（8）

　　其幅频特性表达式为

　（9）

　　其相频特性表达式为

　　　　　　　　　（10）

　　下面着重介绍一阶和二阶系统的动态特性参数。

相关内容推荐：

• 2016-11-22一阶和二阶系统的数学模型