 图1 2ASK信号的时间波形 2ASK信号的产生方法:有键控法和模拟调制法,如图2所示。
图1 2ASK信号的时间波形 2ASK信号的产生方法:有键控法和模拟调制法,如图2所示。  图2 2ASK信号的产生 2.功率谱密度和带宽
图2 2ASK信号的产生 2.功率谱密度和带宽 当概率
当概率 功率谱密度示意图
功率谱密度示意图  图3 2ASK信号的功率谱密度示意图 (1)因为2ASK信号的功率谱密度
图3 2ASK信号的功率谱密度示意图 (1)因为2ASK信号的功率谱密度 图4 2ASK信号的包络检波 由图4可见,在2ASK信号的非相干接收中,包络检波器、低通滤波器的输出送到抽样判决器。根据判决门限电平,在抽样时刻判决脉冲的有无。因此,计算非相干ASK系统的误码率,就需要确定抽样判决器前传送“1”信号时信号加噪声合成包络的概率密度函数,以及传“0”信号时噪声包络的概率密度函数,然后再根据判决门限,确定非相干系统的误码率。
图4 2ASK信号的包络检波 由图4可见,在2ASK信号的非相干接收中,包络检波器、低通滤波器的输出送到抽样判决器。根据判决门限电平,在抽样时刻判决脉冲的有无。因此,计算非相干ASK系统的误码率,就需要确定抽样判决器前传送“1”信号时信号加噪声合成包络的概率密度函数,以及传“0”信号时噪声包络的概率密度函数,然后再根据判决门限,确定非相干系统的误码率。 图6 包络检波时误码率的几何表示 (1)当发送的码元为“1”时,错误接收的概率即是包络值
图6 包络检波时误码率的几何表示 (1)当发送的码元为“1”时,错误接收的概率即是包络值 上式中的积分值引入Marcum Q函数计算,Marcum Q 函数的定义是
上式中的积分值引入Marcum Q函数计算,Marcum Q 函数的定义是  式中:
式中: 假设发送“1”码的概率为P(1),发送“0”码的概率为P(0),则系统的总误码率为
假设发送“1”码的概率为P(1),发送“0”码的概率为P(0),则系统的总误码率为  式中,第一项是基带信号,第二项为高频成分,经低通滤波器后,可输出
式中,第一项是基带信号,第二项为高频成分,经低通滤波器后,可输出 图5 2ASK信号的相干解调 误码率的求解过程如下,波形经过相干解调器(即乘法器和低通滤波器)后,抽样判决器输入的波形
图5 2ASK信号的相干解调 误码率的求解过程如下,波形经过相干解调器(即乘法器和低通滤波器)后,抽样判决器输入的波形 当发送信号“0”时,
当发送信号“0”时, 图7 相干解调时误码率的几何表示 若仍令判决门限为
图7 相干解调时误码率的几何表示 若仍令判决门限为 其中
其中 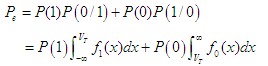 可知,当
可知,当 当
当全站搜索